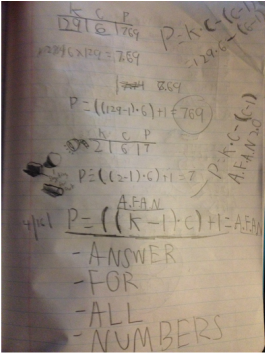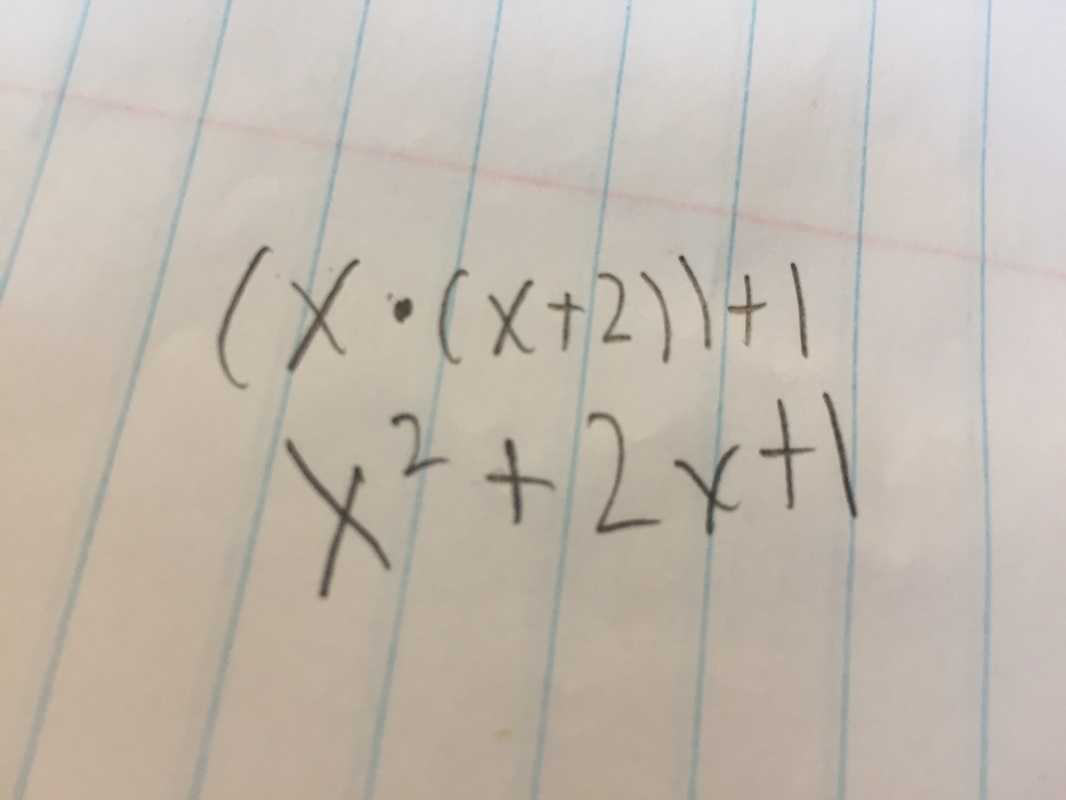Problem of the Week #1: Four 4s
|
As the you may have seen in the title, this problem involves four 4s, or 4 fours. The problem asks for us to see what combination of numbers will result in different outcomes. For example, if I was just playing with the problem and did 4+4+4+4 I would get the answer 16. This mean I have found that the number 16, can be written as 4+4+4+4. We were supposed to write out several different equations and possibilities that we were able to produce.
My process was relatively simple, it consisted of only four steps. My first step was to merely understand the tools I would have at my disposal. In this case it would be all the different types of math symbols such as factorials and square roots. Interestingly enough I learned how factorials work and what they are through this project. So that was excellent as well. The second step was to simply think of anything. Anything what would give me an answer between the numbers 1-100. For example if I was just testing different theories and came up with 4! + √4 - 4/4 = 25, then I would be able to check the number 25 off because I have found a way to create that number using only, four 4s. The third step was simply to record everything so that I could learn continue to find more answers with ease. Every answer I was able to create made it all easier for me. |
I believe that there is no real solution to a problem like this mainly due to the fact that there are several mini-problems and each have so many have several solutions. So to begin I just began writing random sets of numbers and seeing where they would take me. I learned new things from each and was able to complicate each equation just a little bit more. After that I tried to find a set amount of numbers. So from the numbers 1-25 I attempted to find at least one equation that would equal that number. If I created an answer and tested that it worked I just kept it and made sure I had it written.
|
To conclude this problem, I simply want to explain what I've learned from this project, and how I believe I worked throughout the project. Now, I learned quite a bit in this project. But the most significant thing I think I learned was how some answers can be put together. This problem has really opened my eyes to see how Math is actually infinite in a way. Of course I also learned things like factorials and how they work but I think that learning about the true limits of math is a lot more important. One Habit of a Mathematician I think was crucial to solving this problem was being Systematic. This helped me with the first part of really figuring out what ways I could do things and where those plans would lead.
If I were to give myself a grade it would a 10/10. I believe this because in my opinion I believe I was able to understand this problem thoroughly and how it works. I also met all the requirements, and would like to think I did more than what was asked of me. |
Problem of the Week #2: The Gumball Dilemma
This problem was appropriately named "The Gumball Problem" due to the fact that it is a dilemma involving gumballs. The problem begins with a woman named Ms. Hernandez, who happens to have twins. Ms. Hernandez and her twins were out doing stuff and they come across a gumball machine that has two different color gumballs inside. The twins, of course want the same color gumball, so the problem then asks us why it is that Ms. Hernandez should only have to spend three cent. Now, to represent this problem on a keyboard I am going to be replacing the colors with two different letters.
The twins want the same color gumball, from a machine that has only two color gumballs. Why is three cents the most Ms. Hernandez would have to spend? Well let's say the two colors in the gumball machine were B(Blue) and R(red), Ms. Hernandez would only need to get two of one color. The reason she would at maximum have to spend three cents is because with the first two cents she would most likely get a B gumball and a R gumball. So if she got one of each. She would be able to complete a pair using only one cent. B, R/B or R. That is why she would only have to spend two cents. Now the problem goes on to explain a similar problem but with different scenarios which is why I am not going to get into them.
The twins want the same color gumball, from a machine that has only two color gumballs. Why is three cents the most Ms. Hernandez would have to spend? Well let's say the two colors in the gumball machine were B(Blue) and R(red), Ms. Hernandez would only need to get two of one color. The reason she would at maximum have to spend three cents is because with the first two cents she would most likely get a B gumball and a R gumball. So if she got one of each. She would be able to complete a pair using only one cent. B, R/B or R. That is why she would only have to spend two cents. Now the problem goes on to explain a similar problem but with different scenarios which is why I am not going to get into them.
|
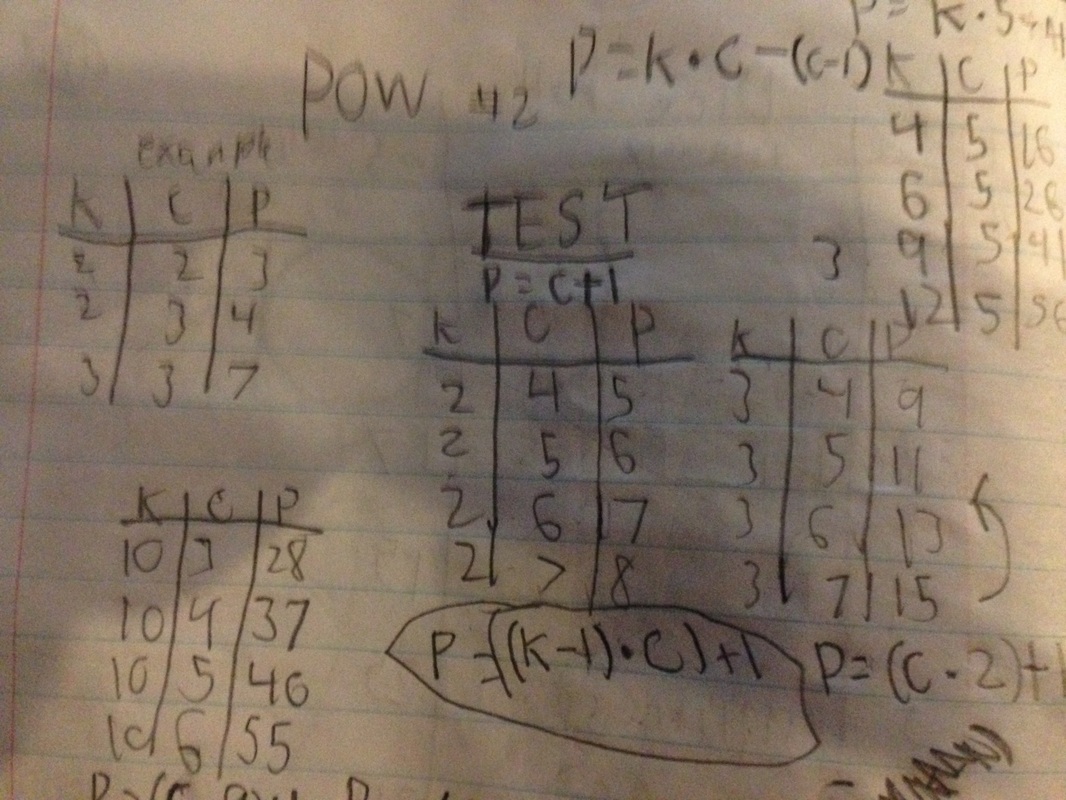
This is how I began the problem, most obviously I spent no time attempting to better understand the problem and went right into the end goal. The end goal was, as stated on the paper," to find a formula so that, if someone tells you the number of colors and the number of children, your formula will tell you the maximum amount of money that the parent might need to spend." So of course I decided that the best I could do was play around with it. So I conducted several tests and attempted to notice several patterns involved with the amount of colored gumballs in the machine, the amount of children and the pennies it took.
As I worked I of course began to notice certain patterns, for example. I noticed that when there was a constant of two kids, and no matter how many colors I chose to have in the gumball machine, it would always be the amount of colors, plus one. So if I had four colors, it would be a maximum of five pennies. Or if I put seven colors, it would be a maximum of eight pennies spent. And so on. I did this and found the correlation for the constant of three children, and ten children. Until I found something, awesome. |
|
Now to the left you can see the work of a math student whose mind is running with wild conclusions. It may look like a lot, and it is. You may be able to spot a large series of letter, and these letters say the following.
P=((k-1 x c) + 1 = A.F.A.N A.F.A.N -Answer -For -All -Numbers And yes that is what I named the equation that I had created. It is a working equation that is able to solve any of number of children or gumballs and pennies if units are plugged in correctly. Now to explain why this equation works and the reasoning behind such, to me, would be impossible because it just does. I did happen to test it, as you may see at the top. I plugged in 129 children, 6 colors and I should have gotten the number 769 for the number of pennies used. And I did, so I was fully able to say that this equation works, because it does. I also came up with a second equation, P= k x c - (c - 1). Once again, same thing as the other, found through patterns and uncomprehending to me why it works. |
This problem was much definitely a bit simpler than the last. This is mainly because of the fact that this problem can be solved simply by looking at patterns and placing them together. Kind of like a puzzle, with a lot of pieces that don't mix well. It was definitely pretty easy finding these patterns, especially in the individual tests themselves. Although the hard part was seeing and looking for the correlation between all of these patterns and how they could possibly mixed together. Luckily it was doable and I did it not once, but twice! So overall I had quite an enjoyable time finding all of those "Aha!" moments, where I was able to find those patterns and how to place them together. If I was to chose one habit of a mathematician to say I used I would say that "Looking for Patterns" was most definitely the biggest habit used in this problem. For obvious seasons of course. So if I was to grade myself on this problem I would say 10/10, and that is because I do think I filled the requirements for this grade, and was able to just take that extra step in finding an alternative (and maybe even simpler) way of solving the same problem. That concludes my work on the "Gumball Dilemma".
Problem of the Week #3: Just Count The Pegs
POW #3 took us through the great journey of finding equations to find the area of different categories of polygons. Most of these shapes were created on a Geo-Board, which is a board with several pegs that a person uses rubber bands to stretch across these pegs. In this problem we have three very interestingly-named characters attempting to find equations that would figure out the area of any polygon on a Geo-Board. The first, Freddie Short says he has a formula that could find the area of any polygon that has no pegs on the interior. The second character, Sally Shorter says she can find the area for any polygon with exactly four pegs on the borders. She just needs to know the number of pegs on the inside. Our final character, and arguably brightest character, Frashy Shortest says she has the equation to rule them all. She can find the area of ANY polygon, she simply needs to know how many inside and outside pegs there are. Now my task was to find these equations and more, starting from the simplest to hardest.
|
To the left is the worksheet explaining everything I wrote above. But below you can see the basic problem layout for the rest of the POW. First it asks us to find the person's formula, then find a variation of it with different conditions. Then again, after which is asks us to repeat the process with different numbers. That is the format for problems 1-2, which are the only problems. Of course, we do later still have to find Frashy's formula. To find all the formulas that I did I used the very simply method of looking at patterns and testing. I would create several different polygons that fit the conditions of the problem and take a look at the numbers and create an equation. Then go on to test that equation with several other polygons. That was how I figured out all of the formulas that I found, simply through observation and thought. |
|
The answers to several of the required scenarios can be found to the right of this text. So can my organization for finding the final equation. I arranged and wrote what conditions they required to fit under. And of course I wrote down the "Best-Equation" down below along with it's variables. This problem was again, just like the rest, very enjoyable and informative to the way equations work and are arranged. Although I do feel that most of these POWs are getting repetitive I still find enjoyment in doing them and figuring out these equations. As Mr. Corner, my teacher would say, I enjoy feeling like the Mathematicians of old times, discovering something for the first time and saying "I figured this out!". That's always the best part of these problems.
Of course as most POWs go I feel I strongly used the "Looking for Patterns" Habit of a Mathematician most because all of my work was patterns and figuring out equations. So to finish this off I believe this was my best work done by far, as I was able to complete the task well and efficiently. I can only say I'm excited for what the following week will bring. |
Problem of the Week #4: Cutting the Pie
In this Problem of the Week we dealt with cutting and separating circles into as many pieces as the cuts will allow us. Basically, we if we were cutting a pie into as many pieces as we could, even in the pieces aren't all even. Every piece matters!
We were asked to explore this concept and delve as deep into it as we could. We would explore all the different cuts that there are, find patterns between the total number of pieces and the number of cuts and even create a formula to finding any amount of maximum pieces using only the number of cuts as a variable.
We were asked to explore this concept and delve as deep into it as we could. We would explore all the different cuts that there are, find patterns between the total number of pieces and the number of cuts and even create a formula to finding any amount of maximum pieces using only the number of cuts as a variable.
|
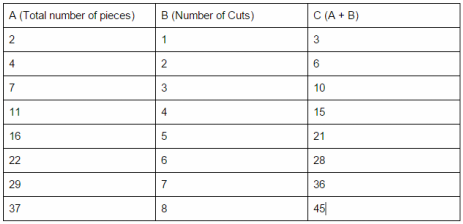
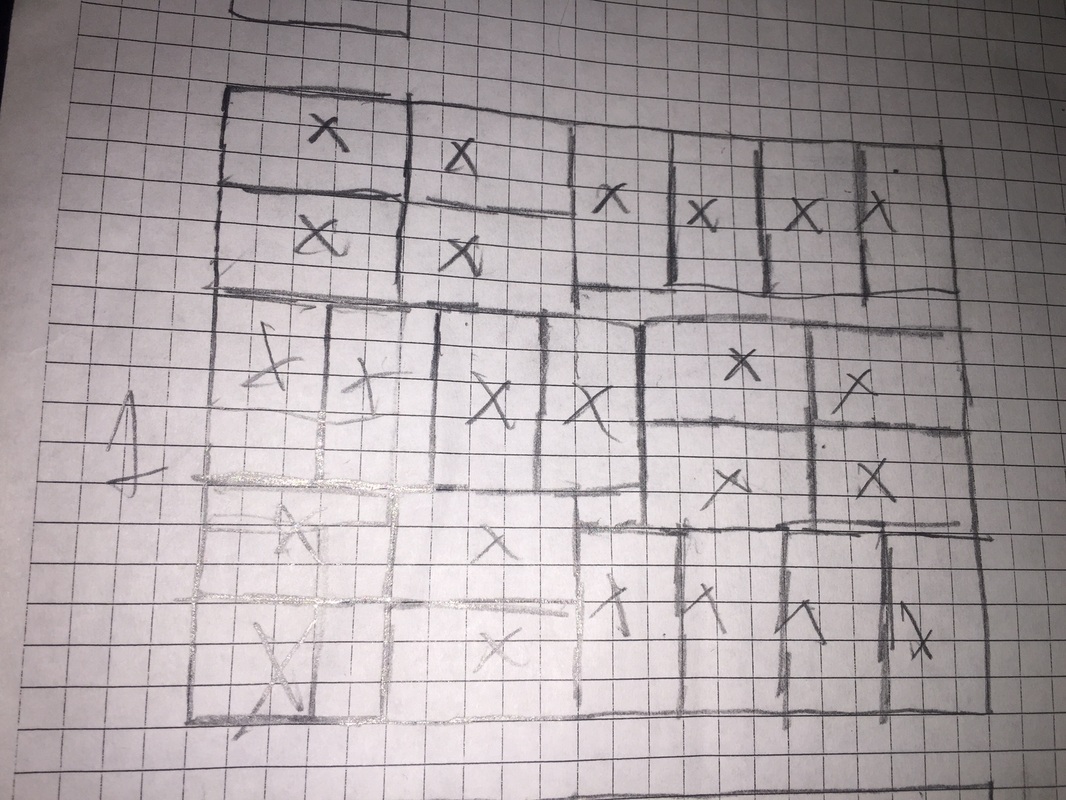
When we were thrown into this problem we began with just some basic examples such as finding the total amount of pieces with two, or three cuts. Then going on from there we began to have a little more trouble. Mainly due to the fact that the more cuts make it a little more difficult. I was able to gather the following information which I thought was more than enough to ultimately find an equation for.
To the Left is a table with Sections A, B and C. A represents the Total number of pieces from B, which is the total number of cuts. Then C, represents the addition of these two. Which may seem weird and totally unnecessary, but it is. It is necessary for the equation that I found because if you could not tell the total for A and B is always one less, than the next A. For example, with three cuts, the addition of A and B is 10. And with four cuts, A is 11, which is only one more than 10. Same goes for all of the other amount of cuts. So I took this information and was able to create and equation. |
The final equation took into account the theory explained above and simple division and multiplication.
((((x - 1) / 2) +1) x 6) +1
That should be able to find any amount of total pieces for any number of cuts as long as you can do the Math.
What I learned from this POW was simply another way to look at certain events and I've definitely grown in the area of finding patterns and creating formulas definitely due to all of the POW's being revolved around that idea. Other than that I can't really say I've learned much more. I was able to do this simply by investigating and finding patterns and that's almost all that I did. In fact, this Problem of the Week took me less time than any other. I would believe that it is because I have gotten much better at them but also because they all seem to be so similar. That is one thing I really hope to see improve in the upcoming POW's. Different types of problems and types of solutions, because most problems have just ended up being a big pool of patterns with a formula as a solution. Which is why you might guess I used the "Looking for patterns" Habit of a Mathematician to solve the problem.
To finalize this POW I would like to say that I believe I deserve a 10/10, due to the efficiency and work that was placed into this problem. Though I am not afraid to say that unlike most POW's I am beginning to grow quite tiresome and even bored of this type of work,
((((x - 1) / 2) +1) x 6) +1
That should be able to find any amount of total pieces for any number of cuts as long as you can do the Math.
What I learned from this POW was simply another way to look at certain events and I've definitely grown in the area of finding patterns and creating formulas definitely due to all of the POW's being revolved around that idea. Other than that I can't really say I've learned much more. I was able to do this simply by investigating and finding patterns and that's almost all that I did. In fact, this Problem of the Week took me less time than any other. I would believe that it is because I have gotten much better at them but also because they all seem to be so similar. That is one thing I really hope to see improve in the upcoming POW's. Different types of problems and types of solutions, because most problems have just ended up being a big pool of patterns with a formula as a solution. Which is why you might guess I used the "Looking for patterns" Habit of a Mathematician to solve the problem.
To finalize this POW I would like to say that I believe I deserve a 10/10, due to the efficiency and work that was placed into this problem. Though I am not afraid to say that unlike most POW's I am beginning to grow quite tiresome and even bored of this type of work,
Problem of the Week #5: Possible Patches
This week's problem involved the fashion genius of Ralph Lauren and his process with how he cuts his cloth. We were given several examples of different sizes of cloth that Ralph Lauren had at his disposal and the necessary size of each cloth he was cutting. The problem, unlike most, used proof to find answers. As Mr. Corner wrote down, "the proof is on the paper". This encouraged us to try and actually write down the examples to find the answers. And luckily for me that's exactly where I found them.
|
The first example was using a large 17 by 22 inch piece of satin. We were instructed to find out how many 3 by 5 pieces we could get from the satin. It took a bit of planning and math calculations to find out how many pieces we could get. Of course I tried to find the maximum number of pieces we could cut from the satin, so I'm sure there are other ways of cutting it that might give a lower of equal number of pieces.
|
|
The rest of the examples were fairly simple where we had to draw it out to finally get to the answers we were looking for. In the following problems I had been looking for the maximum amount of pieces that we could get from these different sized cloths. On the little slideshow to the right there are examples for finding 9 by 10, 5 by 12 and 10 by 12 sized strips from a piece of satin that is 17 by 22 inches in size. There is an example for finding 3 by 5 inch pieces in both 4 by 18 inch satin pieces and 8 by 9 in pieces.
This project like most have started to become mildly stale but still this was an interesting different concept than the previous POW's. Instead of investigating deep into the problem the deepest we would have to go is finding the answer on the paper. That really seems to be the gist of it with this problem. Simply guessing and checking. I hope that the next POW will bring a real week's worth of mental frustration and hard work. |
|
Problem of the Week #6: Canalysis (The Coca Cola Project)
Now unless you've been living under a rock for all your life or had the cruelest parents ever known you've probably had a can of Coca Cola. And regardless of whether you've been living under a rock or not, you've probably never thought about how much time went into designing that can. Now in this problem we used our extensive knowledge of finding volume to find the total volume of the Coca Cola can. Of course you there are little dents in the can here and there but for the problem we assumed that the can is a perfect cylinder.
|
We began by finding the volume of the can which is around 365.3, and from there it only got more complicated. The problem gave us four things which we would use to find the perfect coca cola can's measurements. The original can's dimensions. The original can had a height of 12.1 cm, a radius of 3.1 cm which then gave it a diameter of 6.2 cm. And finally a volume of 365.3. With these dimensions we were able to find cans of different heights and diameters that all had a volume of 365.3. For example I created a can that had a height of 0.5 cm which ended up having a radius of 15.25 cm. To the left is all of the different types of cans.
Now the next step was calculating how much each can would cost if each square centimeter of aluminum costs about $0.00016. Now for one can the differences are minuscule. but when multiplied by ten billion the price difference are in the millions. Then we created a graph which would lead us to the cheapest can. |
If Coca-Cola were to change the design to the cheapest can, considering they sell an average of 19 billions cokes a year, they would make a profit of 38 million dollars per year. Now of course considering Coca Cola is already a billion dollar company would these 38 million make that much of a difference? In my opinion it would not. Because the can which we know and love now is already kind of like a standard can size for the world and all soda companies world-wide. And what would Coca-Cola's CEO's do with 38 million more dollars beside add it to their own stack of cash?
So to conclude this POW I would say that I was able to extend my knowledge in the area of geometry and in calculating area. Specifically of a cylinder. I think that I was able to do this problem effectively and did good work to attempt to find the answer. Which I as well was able to achieve. The Habit of a Mathematician I think I was able to use most effectively was to "Collaborate and Listen" because teamwork was crucial in this problem. Especially when we all gathered to attempt to find the smallest can with the best volume. I had a good time doing this problem and hope to find joy in the next ones to come.
So to conclude this POW I would say that I was able to extend my knowledge in the area of geometry and in calculating area. Specifically of a cylinder. I think that I was able to do this problem effectively and did good work to attempt to find the answer. Which I as well was able to achieve. The Habit of a Mathematician I think I was able to use most effectively was to "Collaborate and Listen" because teamwork was crucial in this problem. Especially when we all gathered to attempt to find the smallest can with the best volume. I had a good time doing this problem and hope to find joy in the next ones to come.
Problem of the Week #7: Growth of Rat Population
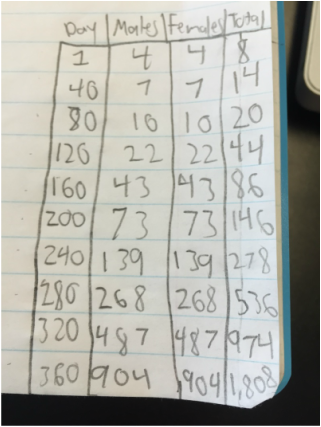
This week's problem of the week involves the growth of a deserted island's Rat population. The problem starts out on January 1st, when two rats, one male and one female, land on an island. On that day the two rats have six kids. Three male and three female. From that day on the female rat will give birth to six kids, three male three female, every forty days. All of the female rats will give birth to six kids starting 120 days from their birth. And from that day on THEY will give birth to six kids every forty days.
In the problem we have to calculate how many rats there are by the end of the year if none of the rats die. I began the problem head-on begging marking out specific times and having a timeline with intervals of 40 days. I began by counting how many rats gave birth each 40 days, which until day 120 was just the original mother. After that it got a little more difficult because I started having to add the children of the children. Which then even after that got more and more confusing. I completed counting how many rats there would be 360 days, or a year, and thought I was complete. I went to check in with my teacher, and surprisingly, I was wrong. I worked this out for a couple hours before I realized there was a much simpler solution.
In the problem we have to calculate how many rats there are by the end of the year if none of the rats die. I began the problem head-on begging marking out specific times and having a timeline with intervals of 40 days. I began by counting how many rats gave birth each 40 days, which until day 120 was just the original mother. After that it got a little more difficult because I started having to add the children of the children. Which then even after that got more and more confusing. I completed counting how many rats there would be 360 days, or a year, and thought I was complete. I went to check in with my teacher, and surprisingly, I was wrong. I worked this out for a couple hours before I realized there was a much simpler solution.
|
I counter up to day 120, where my experiments finally began. I decided that I could find the amount of rats on a certain day, by dividing the amount of rats in total from 120 days before by two, which would give me the total amount of females, and then multiply by six. This would help me find the number of rats born on the day whose total amount of rats I'm trying to find. Surely enough I went all the way through the 360 days with this equation and found the total amount of rats by the end of the year was 1,808. I checked in with my teacher and found that this was certainly the correct answer. I was happy.
I enjoyed this problem because it helped me exercise my problem solving solutions, I was able to see the problem differently and use that to find different ways of solving the problem that were not just simply counting up all the rats. The Habit of a Mathematician that I believe I use most during the POW was most likely Solving a Simpler Problem. Because I was able to take this Week-Long problem and in a sense chop it up to become much easier. More like one equation rather than a problem. |
Problem of the Week #8: Twin Primes
For this Problem of the Week we had a little more liberty. We did not have to specifically find any equation (although finding one was encouraged) and all we really had to do was explore the problem. In this problem we were told that when Twin Primes (3,5 / 5,7 / 17,19) were multiplied were added 1 unit it would come out to be the square of the number in between them. So if we took the numbers 5 and 7 we would 36, which when square rooted is 6. Same with 17 and 19, when we plugged in these numbers and calculated we would get 18 as our answer. Most obviously the first thing I decided to do was find an equation, and that equation was (X x (X+2)) +1. This equation would give us the square of the number in the middle. Though with the help of a friend I was able to refine it and create the following equation X^2 + 2X +1. In case you are confused, X^2 is X squared. I checked as many twin primes as I could just to confirm that I was correct, but then my curiosity told me to attempt the equation with non-prime numbers that were still only two digits apart. Thanks to my curiosity I found that this worked with all numbers. If I used 8 and ten I got 81, which has a square root of 9. If I used 98 and 100 I got 9801 which has a square root of 99. I felt like a mathematical genius finding the answer to the universe.
|
There wasn't much to this Problem of the Week, no real extension or challenge, but there was something special. What made it so great was that there was no definitive goal for me, I didn't have one answer that would solve all my problems. I had to simply explore the dilemma and find whatever I could. You could argue that the goal of this problem was to find the one equation, but I think that was only the beginning. Because through that I was able to find many more ways of working with these twin primes and was able to see that this equation worked with any twin number, prime or not.
The Habit of a Mathematician I used most was most likely "Experiment through Conjecture" because it was through testing that I was able to discover and find equations for my work. All in all it was an enjoyable use of my time and I was glad that I was able to work with this problem. |